이번 글에서는 세상에서 가장 아름다운 수식으로 불리고 있는 오일러 등식,
오일러 항등식에 대해서 알아보도록 하겠다.
인터넷에 찾아보니 테일러 공식을 활용한 유도는 볼 수 있었는데 그걸 하려면
복소 삼각함수 개념을 이해해야 하고, 복소 삼각함수를 이해하려면
또 오일러 공식 (오일러 등식의 뿌리)가 나오기 때문에
이게 원리적으로 맞는 건가? 싶고, 또한 내 기준으로는 더 어렵다고 느끼기도 해서
테일러급수와 수열을 토대로 한 새로운 공식 유도를 해보도록 하겠다.
1. 방법론
가장 먼저, 오일러 등식과 오일러 공식에 대해 구분해줘야 한다.
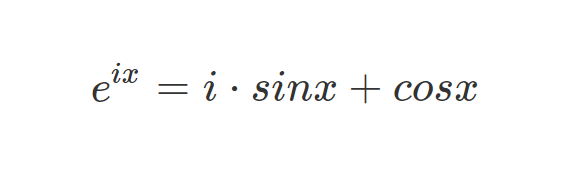
이건 오일러 공식이다.
"공식"이기에 대입할 수 있는 x의 값이 존재한다.
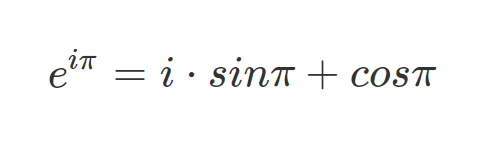
반면, 이건 오일러 등식이다.
원래의 식과 조금 달라 보일 수 있으나 계산하면 우리가 아는 식이 나올 것이다.
이걸 계산하려면 2015 개정 교육과정 기준으로 고2, 수학 1에서 배우는
호도법, 삼각함수 부분을 배워야 한다.
https://alpaca-code.tistory.com/112
각도법(육십분법), 호도법. (차이점, 사용되는 곳)
이번 글에서는 각도 법과 호도법에 대하여 조금 알아보겠다. 먼저, 각도 법과 호도법은 그 사용하는 의미가 모두 회전에 관한 것이다. 이 두 개념은 모두 회전을 위해 사용되는 것이며, 지금부터
alpaca-code.tistory.com
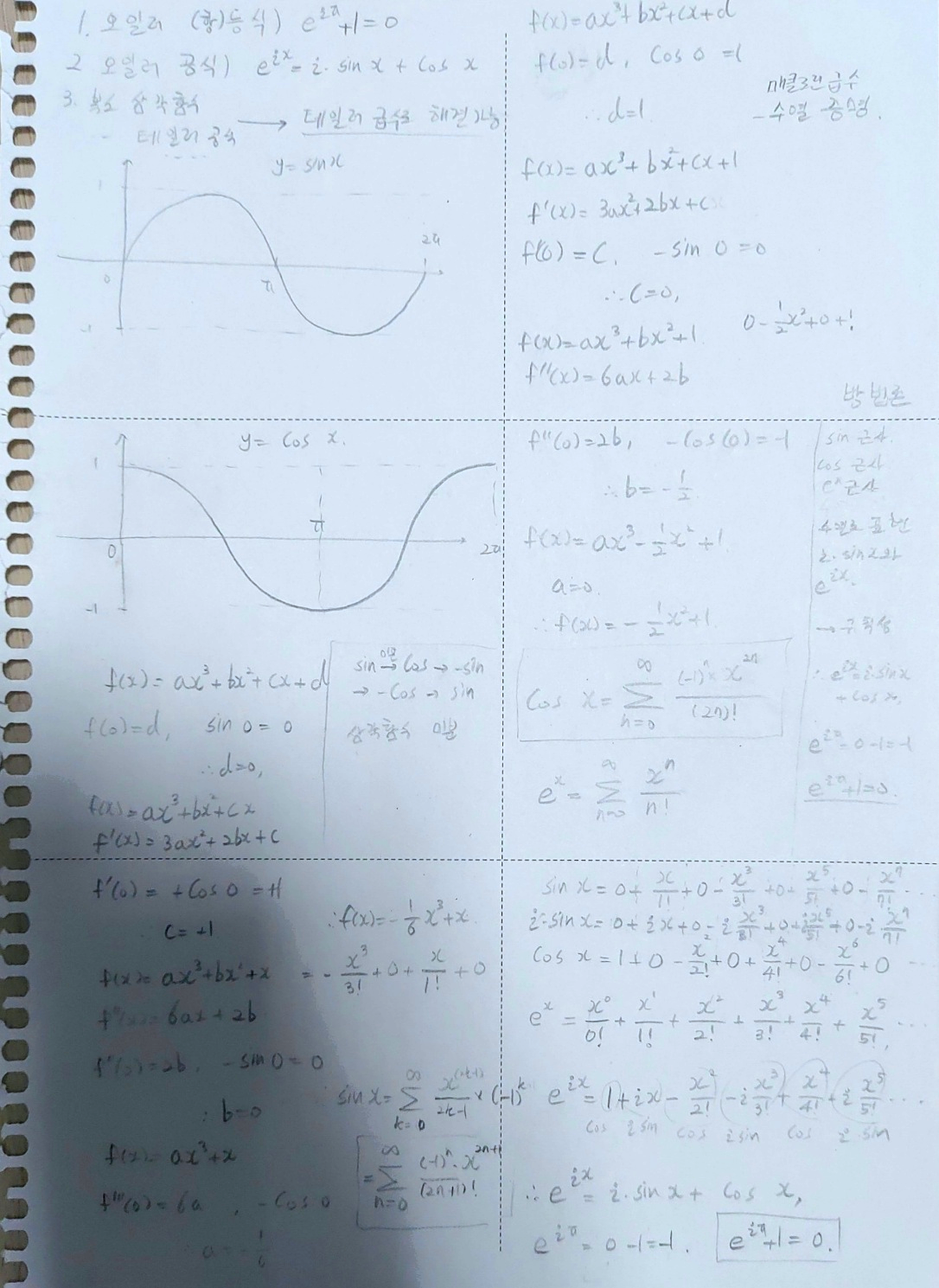
이걸 모르는 상태라면 그래프를 제시해 줄 테니 값을 찾는 방향으로 가보자.
1-1. 사인과 코사인의 값 계산하기.

이건 sin x와 cos x를 그린 그래프이다.
sin 함수는 x = 𝛑/2 (0.5𝛑)에서 1의 최댓값을 갖고, x = 𝛑에서 0의 값을 갖는 형태이다.
따라서 sin는 0의 값을 갖는다.
그리고 0에 i를 곱한 값도 자연스레 0이 되게 된다.
이번엔 cos의 값을 찾아보자.
파란색 선이 cos 함수를 나타낸 건데,
x가 𝛑일 때 값이 -1인걸 볼 수 있다.

따라서 다시 한번 수식으로 나타내주면 위와 같다.

이걸 정리하면 위와 같고,

-1을 좌변으로 넘겨주면 오일러 등식이 탄생한다.
여기까지의 결론은, 우리는 오일러 "공식"을 찾아야 한다는 것이다.
여기서 "찾아야 한다"는 말은 증명이 아닌 유도를 해야 한다는 말이다.
여기서 알아야 할 지식은 테일러급수와 수열인데,
수열은 몰라도 된다. 말만 어렵지 보면 이해가 갈 것이다.
그렇다면 문제는 테일러급수이다.
이걸 이해하려면 미분의 도함수라는 개념의 이해가 동반되어야 하는데,
수학적으로 좋은 방법은 아니지만, 당장 오일러 공식의 유도만 필요하다면
원리 집어치우고 도함수 구하는 법만 알면 되긴 하다.
https://alpaca-code.tistory.com/187
테일러 급수, 매클로린 급수. (정의와 사용방법, 실제 예제)
테일러급수란 무한번 미분 가능한 함수 f(x)에 대해 도함수(미분)를 통한 추측으로 다항함수를 구성해서 f(x)와 근사한 새로운 다항함수를 만드는 과정이다. 그리고 매클로린급수란 대입할 수(중
alpaca-code.tistory.com
이걸 언급하는 이유는 나도 중학교 2학년쯤부터 이러한 수학에 관심을 가지기
시작했는데 모르는 개념이 너무 많아서 모두 원리까지 이해하고 넘어가기에는
힘들어서 주제를 하나씩만 잡고 원리까지는 모르는 걸 다음 주제로 삼는 등
하나씩 진행한 경험이 있기 때문이다.
아무튼 저 글을 보면 사인과 코사인을 다항함수로 나타낼 수 있게 된다.
이걸 나열하고, 더하면 공식이 나오게 된다.
한 번 해보자.
2. 사인 함수 (테일러급수)
https://alpaca-code.tistory.com/187 (테일러 급수)
테일러 급수, 매클로린 급수. (정의와 사용방법, 실제 예제)
테일러급수란 무한번 미분 가능한 함수 f(x)에 대해 도함수(미분)를 통한 추측으로 다항함수를 구성해서 f(x)와 근사한 새로운 다항함수를 만드는 과정이다. 그리고 매클로린급수란 대입할 수(중
alpaca-code.tistory.com
https://alpaca-code.tistory.com/96 (팩토리얼)
수학 !(느낌표) 의미 (계승, 팩토리얼)
수학에 관심을 가즈고 여러 공식을 찾아본 사람이거나 유튜브에서라도 한 번쯤은 숫자 뒤에! 표가 있는 걸 볼 수 있다. 이 느낌표는 놀랐다는 말이 아닌 "팩토리얼" 또는 "계승"이라 읽으며 만약!
alpaca-code.tistory.com
혹시 느낌표가 무슨 의미인지 모른다면 위의 글을 참고하라.
여기서는 코사인 함수를 테일러급수로 전개했는데 사인함수도 똑같은 방법으로 하면 된다.
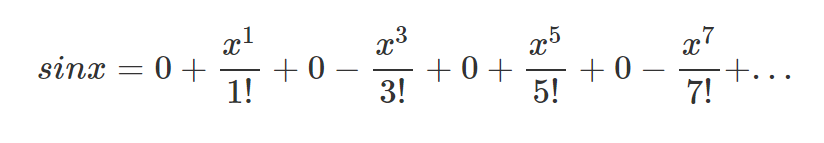
개인적으로도 가장 싫어하는 말이긴 한데, 이해가 되었다는 가정 하에 식을 전개해 보면
위와 같은 수의 나열이 나오게 된다.
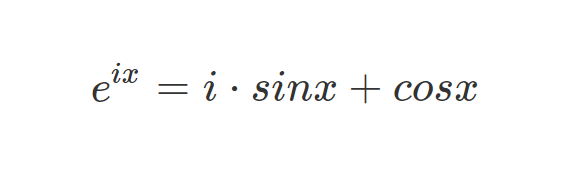
우리는 여기서 사인을 이용하기 위해 이 짓을 하고 있는 것이다.
따라서 sin x 함수 말고, i를 곱해서 i sin x 함수를 표현해봐야 한다.
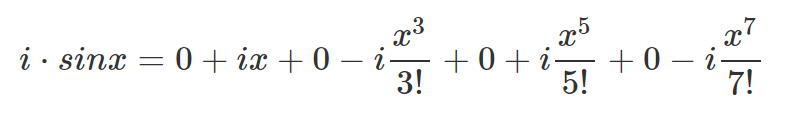
sin x에 i를 곱해서 표현해 보자.
그러면 이렇게 된다. 잘 기억해 두자. 글 마지막쯤에 쓰일 예정이다.
인터넷에 시그마로 표현된 거에서 전개만 해주면 되니까 굳이 전개 안 하고
인터넷에서 찾아보는 것도 추천한다. (이해가 된 가정 하에)
3. 코사인 함수 (테일러급수)
https://alpaca-code.tistory.com/187 (테일러 급수)
테일러 급수, 매클로린 급수. (정의와 사용방법, 실제 예제)
테일러급수란 무한번 미분 가능한 함수 f(x)에 대해 도함수(미분)를 통한 추측으로 다항함수를 구성해서 f(x)와 근사한 새로운 다항함수를 만드는 과정이다. 그리고 매클로린급수란 대입할 수(중
alpaca-code.tistory.com
여기서는 글과 동일한 내용이다.
위의 글을 이해한다면 아래의 사진을 이해할 수 있을 것이다.

사인 함수를 평행이동 하면 코사인 함수가 되기 때문에 어느 정도 유사점이 보일 것이다.

또한 이걸 조금 정리해 보면 위의 식과 같게 된다.
이것도 마무리에 쓰이니까 잘 기억해 두자!
4. 자연 지수함수
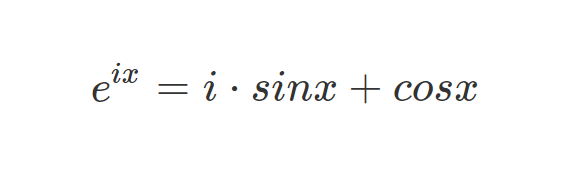
오일러 공식을 유도하기 위해서, e의 ix승 함수를 테일러급수로 표현하면 좋다.
근데 복소 지수를 갖는 함수를 테일러급수 전개하기는 어렵다.
따라서 매우 비슷한 형태인 자연지수 함수, (e의 x승)을 테일러급수 전개하고,
x에 ix를 대입하면 결국 e의 ix승과 같아진다.
자연 지수함수는 어찌 보면 가장 테일러급수로 전개하기 좋은 함수이다.
아무튼, 테일러급수가 이해된다면 이것도 쉽게 할 수 있을 것이다.
팁을 주자면, 자연지수함수를 미분한다면 (도함수가) 자기 자신이 나오게 된다. ( 쉬운 이유 )

이제 e의 ix제곱을 만들기 위해서 x 대신 ix를 넣어보자.

그럼 이런 식이 탄생하게 되는데, i를 계산해 보면 식은 다음과 같이 또다시 전개된다.
(i 제곱은 -1)
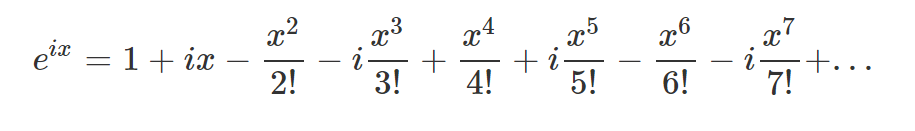
계산하느라 조금 힘들 수 있다.
그래도 계산하면 이렇게 전개된다.
5. 수열 합치기
여기까지 오느라 고생했다.
이제 합치기만 하면 된다.
이 어렵게 구한 3가지 수열을 모두 나란히 놓고 비교해 보자.
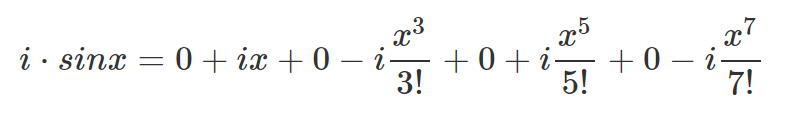

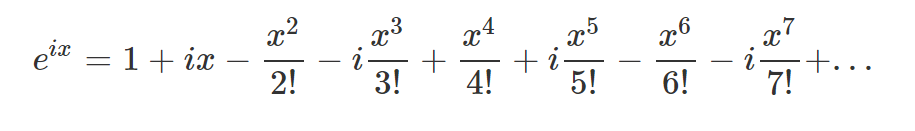
여기서, i sin x와 cos x는 0이 사슬모양으로 배열되어 있다.
따라서 더해주면 각 자리의 숫자가 그대로 배열되는 걸 볼 수 있는데,

이걸 더해주면 e의 ix제곱과 같은 식이 된다!
식의 결과가 같으니 위와 같이 정리해 줄 수 있다.
좌변과 우변을 바꿔주면?

마침내 오일러 공식이 나오게 되는 것이다.
1번 차례인 방법론에서 오일러 "등식"이 나오는 과정을 설명했으니
1번을 안 보고 여기까지 온 사람이 있다면 다시 위로 가서 과정을 보아라.
이게 그렇게 쉬운 과정은 아니지만, 내가 생각하기로는 가장 쉬운 공식 유도법 같다.
물론 경이로운 풀이로 이 공식을 유도할 다른 사람이 생길 수도 있겠지만.
여기까지 오일러 등식 -> 오일러 공식 -> 테일러급수 -> 수열의 합
의 형태로 공식을 유도해 보았다. 물론 아직 많이 어린 수학에
진심인 사람들은 호도법, 팩토리얼 등의 난관도 거쳤을 것이다.
나도 개인적으로 이 주제에 대해서 많이 찾아봤는데,
여러 공식 유도가 있었지만 내가 테일러급수에 대해 알기 때문인지 이 방법이 가장 편해 보였다.
나중에 미분과 적분, 복소 삼각함수, 테일러 공식 등을
모두 이해하게 되는 날이 온다면 다시 한번 다른 유도법을 글로 남기겠다.
이 글로 인해서 한 명이라도 더 공식의 유도 과정을 아는 사람이 생기길 바란다.
원래 이거 세특으로 내려했는데 아직 안 배운 내용이라 못 쓸 것 같다.
글이라도 남아서 세상에 기여하기를 바란다.
이상으로 도움이 되었길 바라며,
끝.
'수학' 카테고리의 다른 글
| 모든 자연수의 합은 음수? - 라마누잔 합 (1) | 2024.12.17 |
|---|---|
| 바젤 문제 증명 (테일러 급수 활용) (1) | 2024.12.17 |
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (증명) (5) | 2024.02.03 |
| 구의 부피 공식 증명 (구분구적법) (2) | 2023.11.06 |
| 자연상수 e. (유래, 계산법, 활용) (2) | 2023.10.25 |







댓글