리만 가설에서 중요한 리만 제타 함수가 나오게 된 역사 중 하나로 바젤 문제가 중요하게 나와서
마지막은 리만 가설로 가는 일환 중 하나로 바젤 문제에 대한 글을 적겠다.

먼저, 바젤 문제란 모든 자연수의 역수의 제곱의 합이 pi^2/6이라는 식을 의미한다.
오일러가 이 식을 알아낸 이후로 제타 함수에 대한 관심도가 증가하여 리만 제타 함수가
만들어지는 데 영향을 주었다는 그런 맥락인데,

위 식은 제타 함수에 2를 넣은 값과 같기 때문에 그런 말이 나오는 것이다.
시그마를 알고 있다면 이해가 갈 것이다. 아무튼, 문제 설명은 이 정도로 하고 증명을 해보도록 하자.

테일러급수를 통해서 sin x를 전개하면 위와 같은 식이 나온다. 인터넷에 찾아보면 시그마로 이루어진
간단한 식도 볼 수 있을 것이며, 테일러급수를 모른다면 아래 링크에서 확인하면 좋을 것이다.
https://alpaca-code.tistory.com/187
테일러 급수, 매클로린 급수. (정의와 사용방법, 실제 예제)
테일러급수란 무한번 미분 가능한 함수 f(x)에 대해 도함수(미분)를 통한 추측으로 다항함수를 구성해서 f(x)와 근사한 새로운 다항함수를 만드는 과정이다. 그리고 매클로린급수란 대입할 수(중
alpaca-code.tistory.com
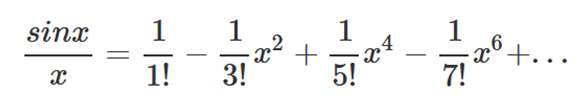
이제 여기서 x로 나눠주자. x의 지수가 1씩 줄어든 것을 확인할 수 있다. 여기까지는 쉬울 것이라고 생각한다.

여기서 sin x의 근을 0, +n𝜋, -n라고 알 수 있는데, x로 나누었으니 0은 제외하고 +n𝜋, -n𝜋만 남아있다.

이것을 다항함수처럼 최고차항의 계수를 a로 놓고 근을 지나가도록 강제한 식으로 표현하면 위와 같다.

이건 근을 통해서 표현한 식 이전에 테일러급수로 유도한 sinx/x 식에서 x에 0을 넣으면 첫째항인 1만 남는 것으로
간단하게 유도할 수 있다. 이를 기억해 두자.

근을 통해서 만든 곱셈식에서 극한을 취했을 때 1이 나오려면 위와 같은 식을 가져야 한다.
이 과정에서 a 또한 1로 정의된다. 여기가 살짝 어려울 수 있는데, 유도를 못하겠으면 대입을 해보고
맞다고 판단하길 바란다.

합차 공식을 이용하면 이렇게 정리할 수 있다.

위 식에서 x^2의 계수를 추측할 수 있게 되는데, 정리하면 우변과 같은 식으로 묶을 수 있다.
그리고 우리는 위에서 같은 식의 또 다른 x^2의 계수를 가지고 있었다. 테일러급수로 전개한 식에서의
-1/3!, 즉 -1/6이 그 대상이다. 이 둘을 같다고 놓으면 바젤 문제가 끝난다.

이렇게 해서 모든 자연수의 역수의 제곱의 합은 pi^2/6 인 것을 알 수가 있다.
물론 오일러가 제시한 첫 증명은 이런 게 아니었지만 나름대로 쉽게 증명할 수 있는 방법 중 하나이다.
이건 리만 가설로 가기 위한 서론쯤에 불과하다. 리만 가설 이해하기라는 보고서를 썼기 때문에
이걸 시작으로 여러 가지 이론이 올라올 것이다. 원래 여기는 느낀 점 같은 걸 적는데 지금은 왠지
생각이 안나는 것 같다. 리만 가설을 주제로 삼아서 그런가 바젤 문제에 큰 흥미가 없는 것 같기도 하다.
바젤 문제가 주제였다면 적을 게 더 많았을 것 같다. 사실 원래도 원리까지는 모르고 있었는데
이번 기회에 쉬운 경로로나마 알 수 있게 되어 기분이 좋다.
이상으로 도움이 되었길 바라며,
끝.
'수학' 카테고리의 다른 글
| 정의역과 공역이 복소수인 그래프를 나타내는 방법 - Domain Coloring (0) | 2024.12.17 |
|---|---|
| 모든 자연수의 합은 음수? - 라마누잔 합 (1) | 2024.12.17 |
| 세상에서 가장 아름다운 수식 - 오일러 (항)등식의 가장 간단한 증명(유도). (0) | 2024.03.20 |
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (증명) (5) | 2024.02.03 |
| 구의 부피 공식 증명 (구분구적법) (2) | 2023.11.06 |







댓글