
중학교 시절, 구의 부피 공식에 대해서 배운 기억이 있을 것이다.
그 증명은 위의 사진과 같고, 간단히 말하면 원기둥에 물을 채우고,
높이를 잰 다음, 원기둥의 부피 공식에 물이 빠진 만큼 곱해주는 방식이다.
따라서 위의 공식이 성립하게 된다.
이 유도 방법은 분명 명쾌하다. 하지만 통계에 기반한 일반화에 가깝다.
그래서 이번 글에서는 좀 더 수학적인 방법으로 공식을 유도해 보겠다.
1. 기본적인 이론
일단 기본적인 이론으로는 "구분구적법"을 사용한다.
"구분구적법"이란, 어떠한 도형의 넓이나 부피를 구하기 위해
무수히 많은 기본도형을 더해 넓이나 부피의 근삿값을 구하는 것을 말한다.

이해가 안 되더라도 괜찮다. 위의 사진을 보자.
이렇게 원기둥을 무수히 많이 쌓아서 즉, n을 무수히 많이 늘려서
(=높이를 0으로 수렴하도록 만들어야 구와 근사해짐)
구의 부피와 같게 만드는 게 이번 글의 기본적인 이론이다.
저 원기둥 하나하나의 부피를 구해서 더해주는 과정을 거쳐야 한다.
2. k번째 원기둥의 부피
먼저, 기본적인 변수를 소개하겠다.
n : 나눌 횟수(원기둥의 개수) , k : k번째 원기둥을 의미하기 위한 변수. (1~n까지의 범위를 가짐) , r : 반지름


먼저, 이 원기둥으로 만든 구를 평면에서 봐보자.
총 5개로 나눠진 걸 볼 수 있다. (n = 5)
또한 반지름은 r이다. 이걸 그림에서 처럼 세로로도 적용할 수 있다.

앞서 말한 구분구적법의 원리에 따라 높이인 h가 0으로 수렴해야 한다.
다시 말해 나중에 n을 극한에 씌워 분모를 무수히 큰 수로 설정하여 0으로 만든다.
이제 우리는 k번째 원기둥의 반지름만 알면 된다.
이건 피타고라스 정리로 구할 수 있다.

삼각형에서 두 변을 알고 있으니 나머지 한 변 즉, k번째 원기둥의 반지름도 알 수 있다.
이제 k번째 원기둥의 부피를 알 수 있게 되었다.
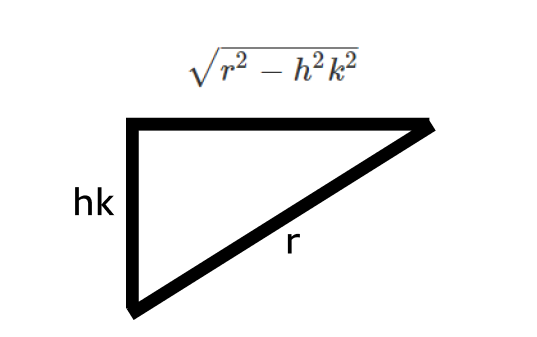
피타고라스 정리를 생각하면, 반지름의 제곱은 r^2 - h^2k^2이고, 높이는 h (r/n)이다.

이걸 토대로, 높이 x (반지름 x 반지름 x pi)로 구해주었다. (h는 r/n으로 바꿔줌)

이걸 살짝 정리해 주면 위와 같은 식이 된다.
최종적으로, k번째 원기둥의 부피는 위의 식과 같다고 말할 수 있다.

3. 구의 부피
1~n번째의 원기둥을 총 n번 더해줘야 한다. k는 "번째"를 의미하기 때문에
1번째 원기둥부터, 나눈 횟수인 n번째 원기둥까지 더해줘야 한다.

이걸 시그마를 이용해 표현하자면 위와 같아진다.

시그마의 기본 성질에 따라서, k와 관련이 없으며
곱해져 있는 위의 식은 시그마 밖으로 빼줄 수 있다.
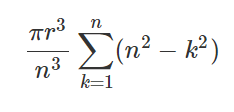
따라서 이런 모습으로 전개되고, 또 시그마의 기본 성질에 따라서,
빼기가 있으면 시그마를 나눠서 처리해 줄 수 있다.

그러면 이렇게 전개해 줄 수 있다.

따로따로 살펴보자. 이 식은 n x n^2 이 되어 n^3이 된다.
이해가 안 된다면 예시를 들어주겠다. 3을 3번 더하라면 무엇인가?
3+3+3 = 9이다. 하지만 3x3으로도 표현할 수 있다.
그렇다. n^2을 n번 더하라는 소리이기에 n과 n^2을 곱해주면 되는 것이다.
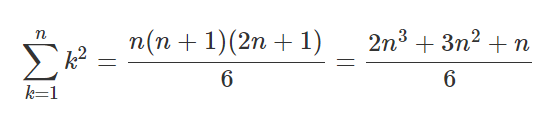
이번엔 k^2쪽을 살펴보자. 이게 무슨 말인지 이해가 안 되는 게 정상이다.
이건 "시그마 공식"으로, k^2 일 때의 공식이다. 원리는 아래 링크를 참고하길 바란다.
https://www.youtube.com/watch?v=kQH2EpuI9VQ (유튜버 "수악중독")
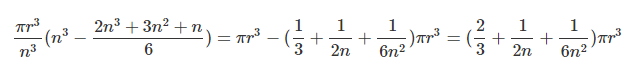
아무튼, 다 전개하고 나면 위의 식이 된다. 이러면 우리는 원기둥 n개로 표현한
근사 구의 부피를 얻게 된 셈이다. 완전한 구의 부피를 얻고 싶으면 어떡해야 할까?

n을 무수히 늘려주면 된다. limit (극한)을 도입해서 n을 무한히 늘리면 위와 같은 식이 된다.
2/3를 제외한 모든 항이 사라지는 이유는 분모가 무수히 커지기 때문이다.
n이 끝없이 커짐에 따라서 n을 분모의 요소로 가지는 (1/2n)과 (1/6n^2)은
분모가 끝없이 커지며 0으로 수렴하게 된다.

여기까지 구했으면 우리는 "반 구"를 구한 것이니
"구"를 구하기 위해서는 2를 곱해주면 공식이 유도된다.
여기까지 중학교 때 보다 훨씬 수학적인 구의 부피 증명법을 알아보았다.
이건 말은 안 해서 그렇지만 적분의 개념과 어느 정도 일치한다.
나도 인터넷을 찾아보며 알 수 있었던 이론이기에
이걸 처음 써먹은 수학자가 존경스럽기도 하다.
이론까지만 보고 직접 증명하려고 며칠 동안 노력했다.
n을 무수히 늘리는 과정에서 n을 분모로 가진 항들이 존재해 줘서 고마웠다.
그래서 이런 증명방법은 몇 가지 경우에만 한하여 가능한 게 아닌가 싶기도 하다.
시험이 끝나고도 구분적분법에 대한 호기심이 남아있다면
원뿔의 부피도 한번 증명해보고 싶기도 하다.
이상으로 도움이 되었길 바라며,
끝.
'수학' 카테고리의 다른 글
| 세상에서 가장 아름다운 수식 - 오일러 (항)등식의 가장 간단한 증명(유도). (0) | 2024.03.20 |
|---|---|
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (증명) (5) | 2024.02.03 |
| 자연상수 e. (유래, 계산법, 활용) (2) | 2023.10.25 |
| 테일러 급수, 매클로린 급수. (정의와 사용방법, 실제 예제) (4) | 2023.10.01 |
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (실험) (2) | 2023.06.04 |







댓글