테일러급수란 무한번 미분 가능한 함수 f(x)에 대해 도함수(미분)를 통한
추측으로 다항함수를 구성해서 f(x)와 근사한 새로운 다항함수를 만드는 과정이다.
그리고 매클로린급수란 대입할 수(중심)를 0으로 놓고 계산하는 테일러급수의 일종이다.
따라서 테일러급수를 알면 매클로린급수도 간단히 이해할 수 있다.
솔직히 이해하기 어렵다. 베이스가 없이 이걸 공부한 사람으로서
글로 있었을 때 이해하기 굉장히 어려웠다. 단어 하나하나씩 뜯어서 보자.
- 무한번 미분 가능한 함수) 말 그대로 미분이 계속해서 가능한 함수를 의미한다.
- 가장 대표적인 함수로는 사인, 코사인 등이 있다.
- 도함수) 이건 한 함수를 미분했을 때 나오는 새로운 함수를 의미한다.
- 참고로 2계 도함수는 함수를 미분했을 때 나오는 도함수를 미분한 도함수이다. (3계, 4계로 이어짐)
- 다항함수) 말 그대로 다항식으로 나타낼 수 있는 모든 함수를 지칭한다. 반례로 사인 코사인 함수등이 있다.
- 근사한) "근사하다"의 수학적 의미는 "비슷하다" 정도로 표현할 수 있다.
이래도 이해가 안 가는 게 맞다고 본다.
나는 직접 테일러급수를 전개하는 영상을 보았을 때 드디어 이해가 갔었기 때문에,
너무 걱정하지 말고 예시를 보자. (코사인의 테일러급수 전개)
가장 대표적인 예시로, 코사인함수에 대한 테일러급수를 전개해서 근사 다항함수를 만들어보자.
1. Cos을 계속 미분하면?
Cos을 미분하면 -Sin이 되고, 그걸 미분하면 -Cos, 그걸 미분하면 다시 Sin이 나오게 된다.
Cos -> -Sin -> -Cos -> Sin -> Cos.... (계속 미분 가능, 순환함)
2. 0을 대입했을 때.
만약 근사 다항함수 f(x)를 ax^2 + bx + c라고 가정하자.

여기에 0을 대입하면? c가 나오게 된다.

그리고 Cos함수에서, x값이 0일 때, 함숫값은 1이 나오게 된다.

이렇게 우리는 f(x)에서의 상수항. c를 1로 유추할 수 있다.
3. 반복. (1차 항)
이걸 반복하면 된다. 앞서 유추한 c를 1로 놓자.
그럼 f(x)는 ax^2 + bx + 1이다.
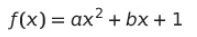
그리고 이걸 미분한 f(x)의 도함수는 2ax + b가 된다.

그리고 Cos의 도함수는 1번에 의해서 -Sin이 된다.

그리고 Cos의 도함수 즉, -Sin에 0을 대입하면 0이 나온다.
이러면 f(x)의 도함수에 0을 넣었을 때 y값이 0이어야 한다.
그러면 2ax + b에 0을 넣어보자.
그럼 당연하게도 x자리에 0이 들어가서 함숫값으로 b가 나오게 된다.

그런데 그게 코사인의 도함수인 -Sin에 0을 넣은 값, 0과 같아야 하기 때문에,

b도 0으로 유추할 수 있게 된다.

4. 반복 (2차 항)
2차 항도 3번과 같이 유추하면 된다.
먼저, 코사인의 도함수의 도함수 즉, 2계 도함수를 알아보자.
1번대로라면 코사인의 도함수의 도함수는 -Sin의 도함수니까 -Cos이 된다. (코사인의 2계 도함수)
그리고 f(x)의 도함수의 도함수, 즉 2계 도함수는 어떨까?
즉, 앞서 구한 2ax + b의 도함수 말이다.
그걸 미분하여 도함수를 구하면 2a가 된다. (f(x)의 2계 도함수)
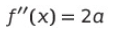
그럼 3번과 같이 코사인의 2계 도함수, 즉 - Cos과 f(x)의 2계 도함수 즉, 2a에 0을 넣어주자.

-Cos에 0을 넣으면 -1이다. (Cos에 0을 넣은 게 1이었기 때문)
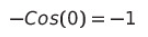
그리고 2a에 0을 넣으면 x가 없기 때문에 그대로 2a이다.

마지막으로 등식을 놓아주면, 2a = -1로 둘 수 있다.

이걸 일차방정식으로 보고 a를 구해주면, a는 -1/2가 된다. (-0.5)

이걸 원래 식인 f(x)에 넣어주자.
5. 결론

그럼 최종적으로 이렇게 된다.
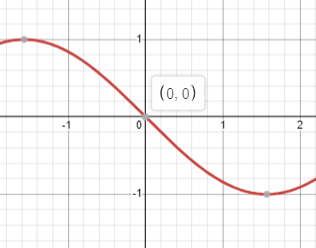
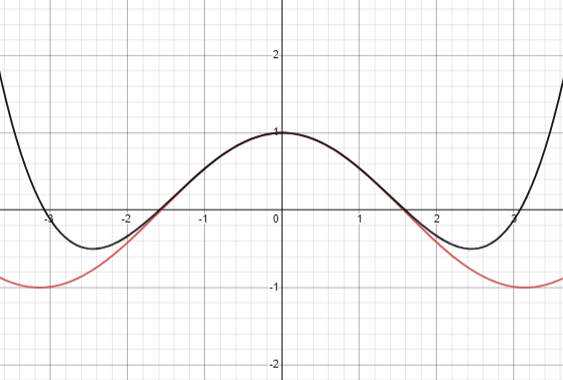
이걸 코사인과 함께 좌표평면에 그려보면 위의 그림과 같다.


중심이 0인 부분에서는 거의 일치하지만, 그 외의 부분은 다름을 알 수 있다.
이건 우리가 중심을 0으로 잡고 0을 대입해서 급수를 전개했기 때문이다.
아무튼 오차를 줄이려면, 이걸 계속 반복하면 된다.
3차 항, 4차 항도 미분을 3번, 4번 즉 3계 도함수, 4계 도함수를 구하고,
등식을 세우면서 항의 계수를 추측하면 점점 더 코사인에 근접해진다.
코사인 함수는 그래프가 반복되기 때문에 일정 구간만 구하면 나머지는 반복으로 처리해도 된다.
아무튼 이렇게 근사 시키는 건 완벽히 똑같이 만드는 게 아니기에
어느 정도의 범위 안에서만 쓰는 조치를 취해야 된다.
저 그래프 또한 -1 ~ 1 외의 범위에서는 오차가 극심해지는 걸 볼 수 있다.
(오차를 줄이려면 3차, 4차 등 계속 계산해나가야 함)

예시만 보여주겠다. 코사인 함수를 테일러급수로 전개할 때, 3차 항의 계수는 0이고,
4차 항의 계수는 1/24이다. 이걸 그래프로 그리면 위와 같다. 좀 더 코사인과 근접해짐을 확인 가능하다.
6. 활용
https://alpaca-code.tistory.com/223
세상에서 가장 아름다운 수식 - 오일러 (항)등식의 가장 간단한 증명(유도).
이번 글에서는 세상에서 가장 아름다운 수식으로 불리고 있는 오일러 등식, 오일러 항등식에 대해서 알아보도록 하겠다. 인터넷에 찾아보니 테일러 공식을 활용한 유도는 볼 수 있었는데 그걸
alpaca-code.tistory.com
테일러급수, 정확히는 매클로린급수가 위의 글에서 활용되었습니다.
사인과 코사인의 수열을 구하는 데에 사용되었습니다.
이 글을 이해하신다면 위의 글도 이해하실 수 있을 겁니다.
관심 있으시다면 한번 보시는 걸 추천드립니다.
여기까지 테일러급수에 대해 적어봤다. 사실 이건 매클로린급수이다. (테일러급수도 맞음)
중심을 0으로 잡았기 때문인데, 이걸 평행이동 시켜서 다른 곳에서 한다고 하면
그건 테일러급수이다. (매클로린급수가 아닌 테일러급수)
아무튼 이렇게 다항함수로 표현할 수 없는 함수들을 근사하게 표현하는
테일러급수를 알아두고 어디에 쓸 수 있을지는 모르겠으나 예시대로
한번 계산해 보는 것도 나름 재밌는 일일지도 모르겠다.
이번 글은 오류가 있을 수도 있겠다고 생각이 든다. 여러 번 체크해 가면서 글을 썼긴 한데,
어디에 옮길 자료라면 이 글은 추천드리지 않고, 오류가 있다면 지적 부탁드립니다.
이상으로 도움이 되었길 바라며,
끝.
'수학' 카테고리의 다른 글
| 구의 부피 공식 증명 (구분구적법) (2) | 2023.11.06 |
|---|---|
| 자연상수 e. (유래, 계산법, 활용) (2) | 2023.10.25 |
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (실험) (2) | 2023.06.04 |
| 한국 수학 개념 영어 표기방법. (0) | 2023.01.28 |
| 0은 짝수인가? (0) | 2023.01.16 |







댓글