
리만 가설에 대해서 찾아본 사람이라면 위 그래프를 한 번쯤 봤을 것이다.
리만 제타 함수를 Domain Coloring이라는 기법을 통해 그래프로 표현한 것인데,
이번 글에선 Domain Coloring에 대해서 알아보겠다.
우선 입출력이 복소수인 함수는 사실 일반적인 방법으로 표현하려면 차원 4개가 필요하다.
복소평면에서 복소수의 위치를 나타낼 때 실수부와 허수부를 x와 y처럼 표현하는데,
출력도 2차원으로 표현하려면 4차원의 그래프가 나와야 한다.
하지만 4차원 그래프는 그리기도 어렵고 봐도 뭔지 모를 것이기 때문에, 아니 사실 볼 수가 없기 때문에
다양한 기법을 통해서 2차원이나 3차원 그래프로 가둬두게 된다.
2차원으로 가두는 방법 중 하나는 Domain Coloring이며, 설명을 시작하겠다.
일단 말했듯 원래는 4차원이 필요한데, 입력한 복소수의 실수부와 허수부는 일반 복소평면처럼
표현하고 출력되는 복소수의 특성 중 편각과 길이를 이용해 각각 명도와 색상으로 바꿔 점으로 표현한 그래프이다.
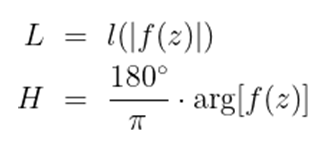
즉, 출력을 좌표 대신 명도와 색상을 조절하겠다는 의미이다. 이걸 결정하는 식은 위와 같다.
함숫값도 복소수라는 것을 기억하자. |f(z)|는 복소수의 크기인데, 복소평면 상에 점을 나타냈을 때
원점으로부터의 길이이다.

복소평면에서의 좌표 찍는 방법과 피타고라스 정리를 안다면 쉽게 이해할 수 있을 것이다.
편각은 실수축과 저 선분 OZ 사이의 각을 의미한다. arg [f(z)]로 표현되었고, arg가 편각의 기호다.

l 함수는 양의 실수 r을 흑백 명도로 바꿔주는 어떤 함수라고 한다.
따라서 다양한 식이 존재하며, 양수를 명도로 치환하는 함수라고 보면 된다.
이렇듯 복소수의 고유 특성 중 2가지, 편각과 크기를 통해서 명도와 색상으로 변환하여
추가할 수 없는 2차원을 색으로 대체하는 아이디어를 통해 그래프가 완성되었다고 보면 된다.
여기까지 Domain Coloring에 대해서 알아봤다.
분량이 애매한 것 같아서 추가로 다른 그래프도 대충 설명하고 넘어가겠다.

이런 3차원 그래프는 입력은 마찬가지로 x, y로 표현하되 z 축은 출력되는 복소수의
실수부나 허수부를 사용해서 나타낸다. 나는 Domain Coloring이 조금 더 낫지 않나 싶다.
실수부나 허수부를 포기하는 건데 의미가 조금 사라질 것 같아서 말이다.
5차원 이상이 필요하다면 Domain Coloring과 3차원 그래프를 섞으면 가능하지 않을까?
방금 생각한 건데 획기적인 것 같다. 그러고 보니 위 그래프도 색이 있다. 이미 있는 방식인가?
이상으로 도움이 되었길 바라며,
끝.
'수학' 카테고리의 다른 글
| 리만 가설 이해하기 (3) | 2025.07.29 |
|---|---|
| 모든 자연수의 합은 음수? - 라마누잔 합 (1) | 2024.12.17 |
| 바젤 문제 증명 (테일러 급수 활용) (1) | 2024.12.17 |
| 세상에서 가장 아름다운 수식 - 오일러 (항)등식의 가장 간단한 증명(유도). (0) | 2024.03.20 |
| 수학) 어느 각도의 포물선이 가장 멀리 날아가는가? (증명) (5) | 2024.02.03 |







댓글