우선, 벡터의 곱셉 중 한 종류인 벡터의 내적은 수학이라는 분야 안에 있는 기술 중 하나이지만,
게임 수학 쪽에 좀 더 연관이 있지 않을까 싶어 게임 수학에 대한 글로써 적을 예정이다.
첫 번째로 내적의 정의를 보고 계산방법과 활용 방법을 소개한 후,
유니티에서 실제로 쓰는 모습을 보여주겠다.
1. 내적의 정의
초등학교 때 곱셈이라는 연산을 배워봤을 것이다.
벡터라는 구조체에도 마찬가지로 곱셈 연산이 있다.
내적과 외적이 그 대상이다.
https://alpaca-code.tistory.com/195 (벡터의 외적 글)
벡터의 외적. (정의, 크기 계산법, 계산 방법, 방향 결정법, 활용법)
이번 글에서는 벡터의 외적에 대하여 글을 남기겠다. 벡터의 외적은 기본적으로 벡터의 곱셈이다. 벡터의 곱셈에는 두 종류가 있으며, 내적과 외적이 대상이다. (외적은 기호로 이렇게 표현한다
alpaca-code.tistory.com
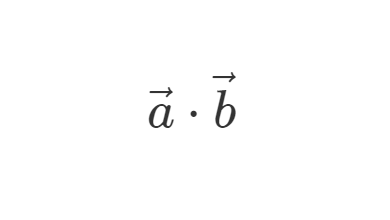
내적은 계산했을 때 실수가 나온다. (스칼라)
내적은 inner product 혹은 dot product라고 불리고, 위의 기호로 나타낸다. (과거의 곱하기 기호)

외적은 계산했을 때 벡터값이 나온다.
외적은 outer product라고 불리고, 위의 기호로 나타낸다. (현대의 곱하기 기호)
예전에 쓰던 곱하기의 기호와 현대 곱하기 기호 두 개를 사용해서
나타낸 걸 누가 했는지 모르겠으나 참 머리가 좋은 것 같다.
만약 곱하기 기호가 한 개였으면 어떤 결과가 초래되었을지 궁금해진다.
이렇게 곱셈이 2개로 나눠졌다는 점은 개인적으로 벡터라는 구조의 특성을 잘 반영한 예인 것 같다.
만약 당신이 과거 수학자였다면 벡터의 곱셈을 뭐라고 정의할 것인가? 일반적인 수는 곱하면 수가 나온다.
벡터도 곱했을 때 벡터가 나와야 할까? 아님 수가 나와야 할까?
이러한 모순을 생각해 보면 벡터의 곱셈이 왜 2가지로 나뉘는지 이해할 수 있을 것이라 생각한다.
2. 벡터의 내적값 계산
벡터의 내적값을 계산하는 방법에는 2가지 종류가 있다.
첫 번째로, 두 벡터의 원소를 모두 알 때의 방법과
두 번째로, 두 벡터의 크기와 사이 각도를 알 때이다.
하나씩 알아보자.
2-1. 두 벡터의 원소를 모두 알 때
벡터의 내적이 무슨 연산인지 아직 기억하고 있는가?
벡터끼리의 "곱셈"이다. 당신이라면 벡터의 곱셈을 어떻게 표현할 것인가? (실수가 나오도록)

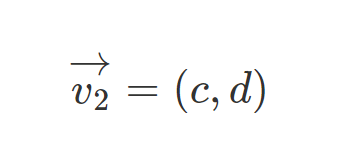
뭐 물론 abcd를 모두 곱할 수도 있겠지만, 현실에서의 벡터 내적은 ab + cd로 표현된다.
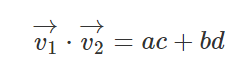
기호를 이용해서 일반화시키면 위의 사진과 같게 된다. (각각 (a, b) (c, d)라는 가정일 때)
첫 번째 방법은 꽤 쉽지 않은가? 두 번째 방법도 그리 어렵지는 않을 것이다.
2-2. 두 벡터의 크기와 사이각을 알 때.
삼각형을 그려 각각의 변을 a, b, c라고 두자.
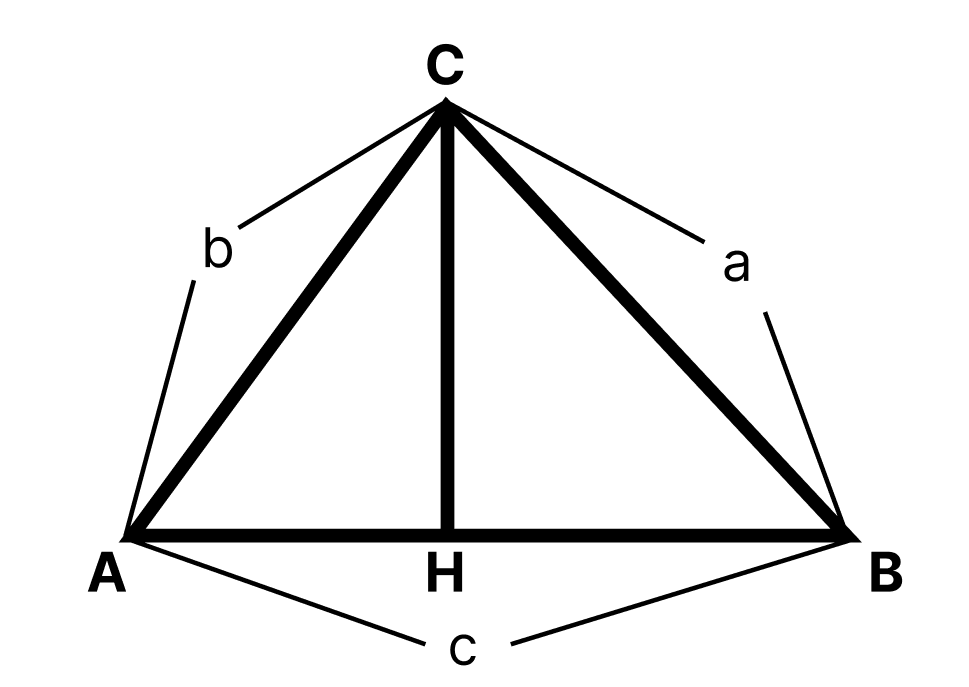
이러한 삼각형에서 연산을 하면 제2코사인 법칙을 유도할 수 있다.
그걸 아래의 사진에 나온 삼각형에 대입하면 내적 공식을 얻을 수 있다.
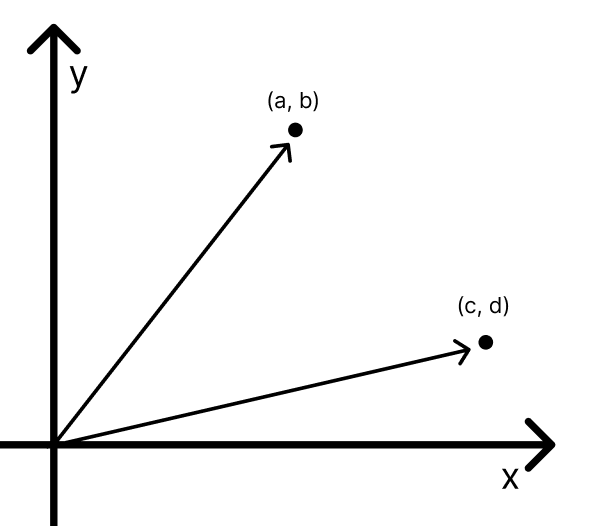

두 벡터를 통해서 삼각형을 만들어주자.
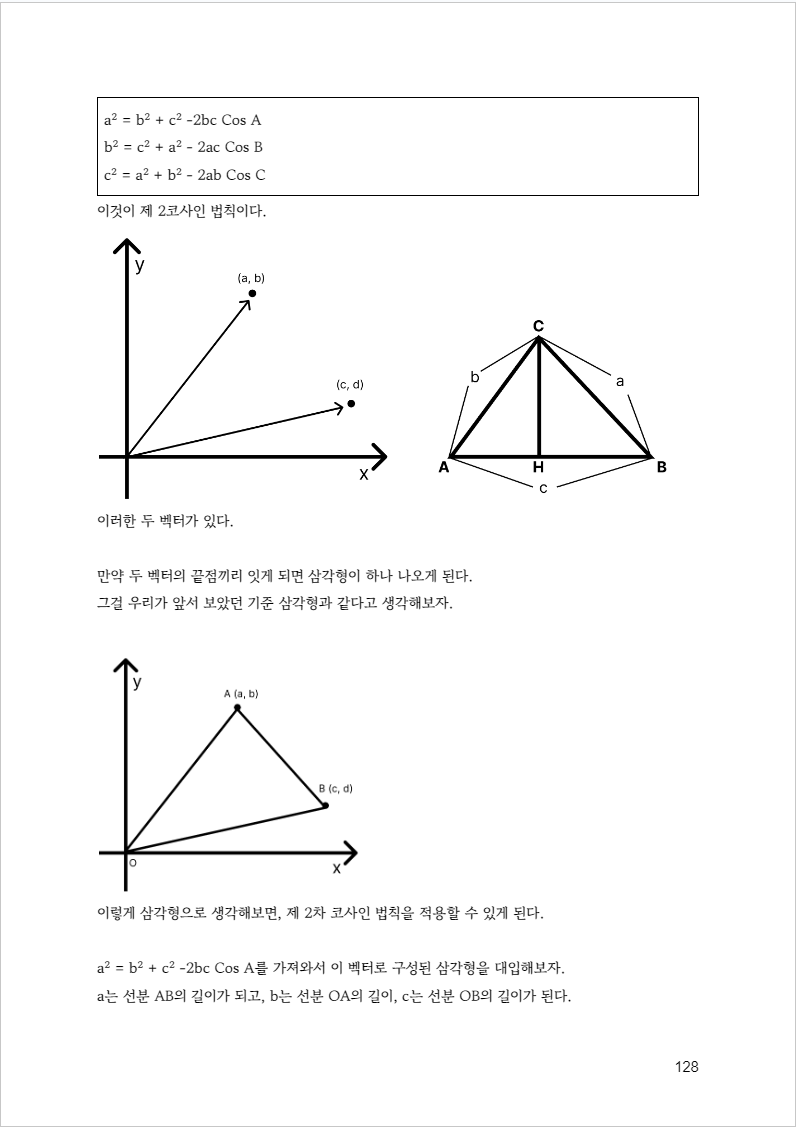


이건 나의 전자책 중 일부이다. (공지에 팔고 있음)
직접 적으면 좋겠지만 귀찮아서 이대로 올린다.
제2 코사인 법칙을 가져와 대입해 주면 저렇게 전개된다.
https://alpaca-code.tistory.com/104
제 2 코사인 법칙. (유도하는 방법)
전 글에서 제1 코사인 법칙을 유도해 보았다. 이번엔 제 2 코사인 법칙을 유도해보겠다. https://alpaca-code.tistory.com/103(이전 글-제1코사인 법칙) 제 1 코사인 법칙. 원래 제 2 코사인 법칙 까지 한번에
alpaca-code.tistory.com
이해가 안 되면 질문하길 바란다. 책에 나름 잘 정리해 놓은 것 같아서 이렇게 올린다.
이 글로 인해서 책이 하나라도 팔리면 참 좋겠지만 아마 대부분이 게임 개발자보다는
그냥 예비 수학자일 것 같아서 딱히 홍보는 안 하겠다.
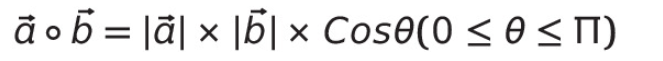
아무튼 다시 공식을 가져와보면 위와 같다.
이제 활용으로 넘어가 보자.
3. 벡터의 내적 활용
같은 값이 나오는 두 개의 공식이 있다는 건 무슨 의미일까?
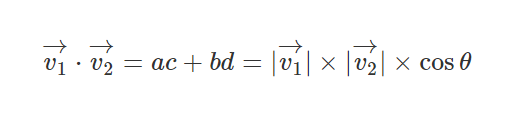
나머지 변수들의 값을 알고 있을 때 원하는 변수의 값을 구할 수 있다는 것이다.
가장 대표적으로, 두 벡터 사이의 각도는 주어지는 경우가 거의 없다. (특히 게임개발에서)
하지만 벡터의 원소, 크기는 보통 구할 수 있는 값이기 때문에 벡터의 내적을 활용하면
두 벡터 사이의 각도를 구할 수 있다!
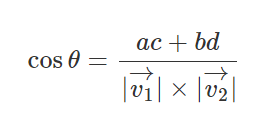
한번 cos에 대한 식으로 식을 변형시켜 보자.

만약에 (0,1)과 (1,0)으로 이루어진 두 벡터가 있다고 가정해 보고
식을 계산하면 위와 같은 결과가 나올 것이다.

따라서 cos θ = 0이라면, y값이 0인 것과 같으니까 0도부터 𝜋(180도)까지 중에는
θ = 𝜋/2이다. 이걸 육십분법(각도)으로 환산하면 90도이고,
https://alpaca-code.tistory.com/112 (파이가 붙은 수의 의미를 모르겠다면..)
각도법(육십분법), 호도법. (차이점, 사용되는 곳)
이번 글에서는 각도 법과 호도법에 대하여 조금 알아보겠다. 먼저, 각도 법과 호도법은 그 사용하는 의미가 모두 회전에 관한 것이다. 이 두 개념은 모두 회전을 위해 사용되는 것이며, 지금부터
alpaca-code.tistory.com
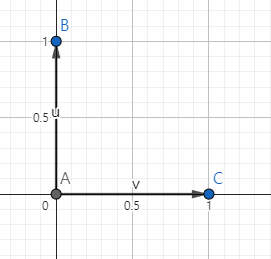
실제로 두 벡터 사이의 각도는 90도인걸 알 수 있다...
이걸 코사인의 역함수로 표현하면 일반각이 아닐 때도 컴퓨터로 계산할 수 있고, 코드로 표현할 수도 있다.
float theta = Mathf.Acos(Vector2.Dot(vec1, vec2) / (vec1.magnitude * vec2.magnitude));
유니티에서는 Vector2.Dot이라는 함수로 내적값을 제공하고,
magnitude라는 값으로 벡터의 크기도 계산해 주기 때문에
이렇게 더욱 쉽게 표현이 가능하다. (Acos = cos의 역함수)
float GetAngleByTwoVector(Vector2 vec1, Vector2 vec2) {
float theta = Mathf.Acos(Vector2.Dot(vec1, vec2) / (vec1.magnitude * vec2.magnitude));
return theta * (180 / Mathf.PI);
}
2개의 벡터를 파라미터로 받는 함수도 만들어뒀으니 알아서 사용하라.
맨 위의 코드는 라디안값으로, 아래의 함수는 실수값으로 결과가 나온다.
여기서는 두 벡터이지만 게임에서는 어떤 기준점(예를 들어 카메라)에서부터의
물체까지가 벡터가 될 수 있다. 그 사이의 각도를 구한다는 것은 카메라를 몇 도
돌려야 다른 물체를 바라보는지 알 수 있는 것과 같다.
이렇게 다양한 분야에 응용이 가능하니까 활용법이라도 알아두길 바란다.
모르면 찾아서 알면 되지만 애초에 이런 게 있는지 조차 모르면
아무것도 할 수 없기 때문이다.
여기까지 벡터의 내적에 대해서 알아보았다. 가장 기초에 근접한 벡터의 내적 글이었다고 생각된다.
제2 코사인 법칙 부분에서 조금 난감할 수도 있을 것 같은데, 그냥 연산하면
저 식이 나오니까 그렇게 집착하지는 않았으면 좋겠다.
벡터의 외적 글이 꽤 잘 나가길래 내적도 한번 적어보았다.
많은 사람에게 지식을 전파할 수 있었으면 좋겠다.
오류나 질문이 있다면 댓글 달아주면 감사하겠다.
이상으로 도움이 되었길 바라며,
끝.
'게임 개발 > 게임수학' 카테고리의 다른 글
| 유니티) 제곱근, n제곱 등 수학적 메서드를 사용하는 방법. (Mathf) (4) | 2024.01.24 |
|---|---|
| 벡터의 외적. (정의, 크기 계산법, 계산 방법, 방향 결정법, 활용법) (1) | 2023.11.03 |
| 오일러각의 정의, 문제점과 사원수의 특징, 사용이유 (0) | 2023.10.12 |
| 게임수학) 게임을 만들때 삼각함수를 쓰는 예. (2) | 2023.01.20 |
| 단위 벡터로 만들기. 벡터 크기 1로 만들기. 벡터의 정규화 하는법. (2) | 2023.01.17 |







댓글