유니티나 언리얼 엔진 등 3차원 세계를 구현해 주는 프로그램에는
회전을 해주는 기능들이 거의 필수적으로 포함되어 있다.
이런 기능들은 표면적으로 오일러 각 체계로 표현되지만,
엔진 내부에서는 사원수로 표현된다. 이 글에서는 이 2가지 체계를 알아본다.
1. 오일러 각
오일러 각 체계는 매우 직관적인데, x, y, z 축을 기준으로 놓고 기준축을 중심으로 회전을 표현한다.
3차원은 축이 3개 존재하기에 이렇게 하면 모든 각도를 표현할 수 있다.

이런 그림으로 보면 편할지 모르겠다. 오히려 어렵게 보이기도 한다.
그렇다면 게임엔진인 유니티로 보여주겠다.

이러한 큐브가 있다. 저기 보이는 3개의 서로 다른 색의 선들은, 축을 기준으로 회전을 해준다.
1. 빨간색 선 회전 (X축)

이렇게 한 개의 축을 기준으로 회전한 걸 볼 수 있다.

X축의 회전이었던걸 확인할 수 있다.
2. 파란색 선 회전 (Z 축)

빨간색 선과 다른 축을 기준으로 회전한 걸 볼 수 있다.
이건 Z 축이다.
3. 노란색 선 회전 (Y축)

이번엔 옆으로 고개를 돌리는 것 같이 회전하는 걸 볼 수 있다.
이건 Y축 회전이다.
아무튼, 이렇게 3개의 축을 놓고 각각의 회전값을 통해서
회전을 구현한 체계가 오일러 각 체계이다.
1-2. 짐벌락 현상
이렇게 완벽해 보이는 오일러 각에도 문제점이 하나 있다.
회전을 해서 두 개 이상의 축이 같아졌을 때 빠져나오지 못하는 문제점이다.
말로 하면 되게 어렵게 보일 수 있다고 생각한다.
하지만 이걸 이해하는 건 생각보다 쉽다.
자료를 보여주겠다.
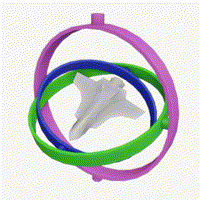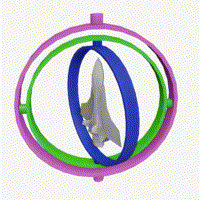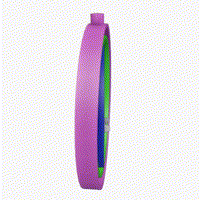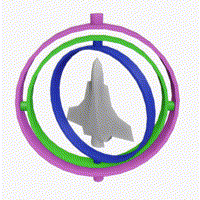
이 영상을 봐라. 원래는 자유자재로 잘 움직이다가, 축들이 하나로 겹치게 되었을 때,
Y축 회전밖에 수행하지 못하는 문제점이 발생하는 걸 볼 수 있다.
저 상태에 갇힌 걸 "Gimbal Lock" 현상이라고 한다.
이 현상 때문에 오일러 각 체계 말고 다른 회전 체계가 필수적으로 사용된다.
제목에도 있었던 사원수가 그 대상이다.
2. 사원수 (Quaternion)
사원수의 정의부터 알아보자.
학교 다닐 때 복소수에 대해서 배웠는가? a + bi의 형태로 표현되며
i라는 허수단위 하나를 가지는 수 체계이다.
2-1. 복소평면에서의 회전, 사원수의 필요 이유
사원수가 회전을 표현하는 수 체계가 된 걸 이해하려면,
복소수를 나타내는 복소평면에서의 복소수의 성질을 봐야 한다.

이런 복소평면이 있다고 가정하자. 1에다가 i를 곱하면 뭐가 되는가?
그렇다 i가 된다. 그걸 그래프 상에 찍어보면, 데카르트 좌표계처럼 봤을 때 (0,1)로 바뀐다.
그럼 (1,0) -> (0,1)로 바뀐 것이니 90도만큼 회전한 것이다.
이걸 요약하면 복소평면에서 어떤 점(복소수)에 i를 곱하면 90도만큼 회전하는 걸 알 수 있다.
그래서 같은 방식으로, 3차원 그래프로 생각하면 i나 j나 k를 곱해줌으로써
3차원에서의 회전을 표현할 수 있기 때문에, 사원수 체계가 도입되어 3차원 회전에 관여하는 것이다.
2-2. 사원수와 삼원수
그런데, 상식적으로 축이 3개 여야 하기에 사원수가 아닌 삼원수여야 하는 게 아닐까?
삼원수는 a + bi + cj의 형태로, 허수단위를 2개 사용한다.(i와 j)
하지만 삼원수는 간단한 계산을 해보면 실수부와 허수부가 혼동되는 모순이 존재하고,
이에 결합법칙, 분배법칙, 교환법칙 모두 성립하지 않는 수임을 보여주며
수학적 의미를 잃어버린 수가 되었다. (역사적으로는 삼원수가 먼저 고안됨)
그래서 수학자들은 허수단위를 하나 더 넣어서 사원수를 만들었다.
a + bi + cj + dk로, i와 j, 그리고 k까지 3개의 허수단위가 존재한다.
사원수는 삼원수와 다르게 곱셈의 교환법칙을 제외하고 모든 법칙이 성립한다.
그러한 이유로 회전체계에는 사원수가 활용되는 것이다.
(또 의미를 가지는 수체계에는 팔(8) 원수, 십육(16) 원수가 있다)
2-3. 사원수의 기본 특성
사원수를 a + bi + cj + dk로 놓고 보았을 때,




이렇게 4개의 등식이 성립한다.
앞서 말했듯이 곱셈의 교환법칙이 성립하지 않는 걸 볼 수 있다.
2-4. 사원수의 회전
사원수의 회전을 구현하기 위해, 예시를 하나 들어보자.
(1, 0, 0)에 해당하는 사원수인 1i + 0j + 0k 즉, i를 회전해 보자.
회전하려면 기준이 되는 축을 곱해준 다음,
노멀라이징을 위해서 같은 수로 나눠주면 된다.
간단하게, j 축으로 1만큼 회전하는 걸 목표로 해보자.
그럼 1+j를 곱해주고, 나눠주면 회전된다.
(실수부를 회전할 값으로 활용한다)
식으로 표현하면,
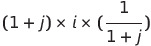
이런 식으로 표현된다.
곱하기 기호를 기준으로 각각 1번, 2번, 3번 식이라 하면
3 번식은 학창 시절 배운 분모의 실수화 기술을 사용하면

이런 식으로 정리된다. (j x j = -1)
이 식으로 바꿔서 앞선 1번, 2 번식과 곱해주면,


결과적으로 -k가 나오게 된다.
따라서 i (1,0,0)을 j 축을 기준으로 1만큼 회전한 결과는
-k (0,0,-1)이다.

이 그래프를 보라. (1,0,0)이 (0,0,-1)로 바뀐 것을 표현한 것이다.
우리가 j 축을 기준으로 1만큼 회전했기 때문에 90도 회전하여 (1,0,0)이 (0,0,-1)로 간 것을 알 수 있다.
또한 1만큼 회전하면 90도만큼 회전하는 것을 알 수 있다.
추가로 사원수는 곱셈의 교환법칙이 성립하지 않기 때문에, 곱할 때 문자의 순서를 신경 써서 적어주어야 한다.
그냥 다항식의 곱셈이고 연산만 많기에
어렵지 않게 이해할 수 있을 것이라 본다.
여기까지 3차원 회전체계 2가지를 알아보았다.
특히 사원수는 엔진 내부에서 많이 사용되니까
이해하긴 힘들더라도 이렇구나~ 정도로 알아두자.
이번 내용은 어려워서 잘못된 정보가 있을 수도 있겠다고
생각된다. 잘못된 점이나 궁금한 점이 있다면 댓글로 달아주면 좋겠다.
이상으로 도움이 되었길 바라며,
끝.
'게임 개발 > 게임수학' 카테고리의 다른 글
| 유니티) 제곱근, n제곱 등 수학적 메서드를 사용하는 방법. (Mathf) (4) | 2024.01.24 |
|---|---|
| 벡터의 외적. (정의, 크기 계산법, 계산 방법, 방향 결정법, 활용법) (1) | 2023.11.03 |
| 게임수학) 게임을 만들때 삼각함수를 쓰는 예. (2) | 2023.01.20 |
| 단위 벡터로 만들기. 벡터 크기 1로 만들기. 벡터의 정규화 하는법. (2) | 2023.01.17 |
| 소박한 집합론(수의 종류,구분) (0) | 2022.11.26 |







댓글