우리가 교육과정에서 배운
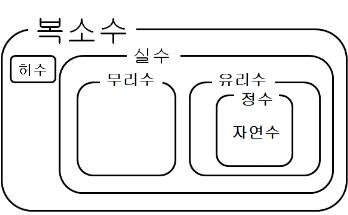
정수, 무리수, 실수, 무리수, 복소수 등
수의 종류들은 사실 이름이 있다.
저렇게 구분하는 식의 이론을 소박한 집합론
이라고 한다.
오늘은 소박한 집합론의 종류와 기호들을 알아보도록 하겠다.
오늘 소개할 종류는 총 7개로,
자연수, 정수, 유리수, 무리수, 실수, 복소수, 사원수 가 있다.
지금부터 하나씩 설명하겠다.
1. 자연수
인간이 가장 먼저 인식한 수의 개념으로
물건을 세거나 순서를 지정할 때 사용하는 수의 집합.
ex) 1,2,3,4,5
2. 정수
자연수와 자연수의 음수(음의 정수), 0을 포함하는 수의 집합.
마이너스가 앞에 붙은 자연수, 자연수, 0을 상징하며
예시로는 1,2,3 , -1 , -2 , -3 , 0 등이 있다.
3. 유리수
분모가 0이 아닌 두 정수의 비율 혹은 분수로 나타낼 수 있는 수의 집합.
분수로 나타낼 수 있는 모든 수를 의미한다.
4. 무리수
두 정수 비 혹은 분수로 나타낼 수 없는 수의 집합.
분수로 나타낼 수 없는 수이며, 가장 많이 접한 무리수로는
원주율(파이)이 있다. 이 수들은 소수점 밑으로 끝없이 이어져 있어
분수 또는 비로 표기할 수 없다.
5. 실수
유리수와 무리수를 모두 포함하는 수의 집합으로,
앞으로 나오는 복소수는 실제로는 존재할 수 없는 반면에
실제 존재하는 마지막 집합이다.
상식적인 수까지의 범위라고 볼 수도 있겠다.
6. 복소수
실수와 제곱하면 -1이 되는 허수 단위 i를 조합해 a + bi 형태로 표현하는 수의 집합.
일단 제곱하면 -1이 되는 허수를 사용하는데,
현실에서 제곱하여 -1이 되는 수는 없음으로
현실이 아닌 수 체계라고 볼 수 있다.
그렇지만 매우 큰 의미를 가진다.(쓸모없다는 뜻이 아님.)
7. 사원수
실수와 제곱하면 -1이 되는 세 허수 단위 i, j, k를 조합해 a + bi + cj + dk 형태로 표현하는 수의 집합.
마찬가지로 허수를 사용하며, 허수 단위가 3개로 주로 4차원에서의 벡터곱을 표현할 때 사용한다.
현실에서 쓸일이 사실상 없으며, 간단히 설명하기 어렵다.
솔직히 이 많은 개념들이 이글 하나로 바로 이해가 딱 될리는 만무하며,
관심이 있다면 조금 더 찾아보길 바란다.
| 분류 | 정의 | 기호 |
| 자연수 | 물건을 세거나 순서를 지정하기 위해 사용하는 수의 집합 | N |
| 정수 | 자연수와 자연수의 음수, 0을 포함하는 수의 집합 | Z |
| 유리수 | 분모가 0이 아닌 두 정수의 비율 혹은 분수로 나타낼 수 있는 수의 집합 | Q |
| 무리수 | 두 정수 비 혹은 분수로 나타낼 수 없는 수의 집합 | I |
| 실수 | 유리수와 무리수를 포함하는 수의 집합 | R |
| 복소수 | 실수와 허수단위 i를 조합해 a + bi 형태로 표현하는 수의 집합 | C |
| 사원수 | 실수와 허수단위 i,j,k를 조합해 a+bi+cj+dk 형태로 표한하는 수의 집합 | H |
이렇게 정리할 수 있겠으며,
이 내용은 이득우의 게임 수학이라는 책에서
발췌한 내용을 정리해 본 내용이다.
앞으로는 수학 관련 게시글이 많을 듯하다.
도움이 되었길 바라며,
끝.
'게임 개발 > 게임수학' 카테고리의 다른 글
| 게임수학) 게임을 만들때 삼각함수를 쓰는 예. (2) | 2023.01.20 |
|---|---|
| 단위 벡터로 만들기. 벡터 크기 1로 만들기. 벡터의 정규화 하는법. (2) | 2023.01.17 |
| 유니티) 2, 3차원에서 적용 가능한 벡터의 정규화 방법. (0) | 2022.11.18 |
| 유니티 콜라츠 추측 계산기 - 2부 (2) | 2022.09.19 |
| 유니티 콜라츠 추측 계산기 - 1부 (0) | 2022.09.19 |







댓글