새로운 주제로 인공지능에 대해서도 공부하기 시작했다.
개인적으로 AI 거품론을 믿고 싶지만 만약 그런 미래가 도래한다면
이것 또한 할 줄 알아야 하지 않을까 하는 마음에 시작하려 한다.
물론 따로 계기가 있긴 하다.
k - 최근접 이웃 알고리즘
그래서 이번엔 가장 쉬운 알고리즘 중 하나인 k - 최근접 이웃 알고리즘에 대해 알아보겠다.
우선 이 알고리즘은 내가 이해하기로 표본들의 분포를 기반으로 가장 비슷한 유형을
추측하는 것이다. 각 표본과의 거리를 비교하여 비슷한 집단을 추측한다.
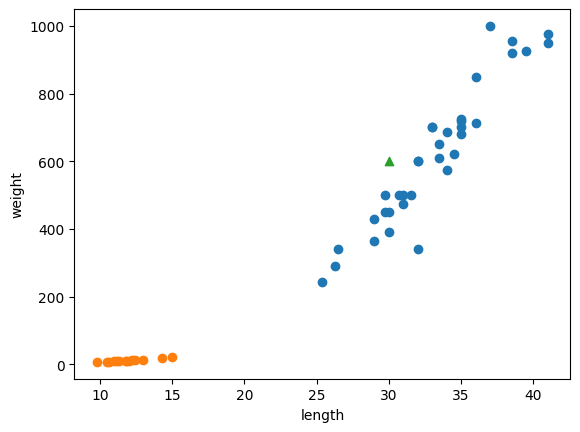
이 두 색의 집단을 보면 한쪽은 도미, 한쪽은 빙어이다.
당연히 왼쪽이 더 작고 가벼운 빙어인데, 세모는 그렇다면 무슨 생선일까?
본능적으로 도미라고 추측할 수 있다. 세모가 도미 집단에 더 가깝기 때문이다.
이렇듯 k 최근접 이웃 알고리즘 또한 거리를 비교하여 가장 유사한 집단을 추측한다.
k 최근접 이웃 알고리즘에 필요한 자료는 데이터가 전부라는 뜻으로도 해석이 가능하다.
한 가지 단점으로는 데이터의 경우가 많을 경우 길이를 모두 비교해야 하기 때문에
연산이 커진다는 정도가 있다고 한다.
따라서 머신러닝이긴 하지만, 훈련의 개념은 아니다. 그런 만큼 이해가 쉬워서
지금 이렇게 기초적인 상태로 소개하고 있는 게 아닐까 싶다.
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
import matplotlib.pyplot as plt
length = bream_length + smelt_length
weight = bream_weight + smelt_weight
fish_data = [[l, w] for l, w in zip(length, weight)]
fish_target = [1]*35 + [0]*14
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier();
kn.fit(fish_data, fish_target);
kn.predict([[30, 600]])
예제코드)
kn.fit() : 알고리즘 학습
kn.predict() : 예측값
여기까지 k 최근접 이웃 알고리즘에 대해서 알아봤다.
KNN이라고도 부르는 것 같다. 앞으로 이런 머신러닝 기법도
올라갈 것 같은데 뭐든 성장하는 것 같아 기분이 좋다.
이상으로 도움이 되었길 바라며,
끝.
'머신러닝' 카테고리의 다른 글
| 머신 러닝) padding, same (0) | 2024.12.25 |
|---|---|
| 머신 러닝) 필터와 커널 (0) | 2024.12.25 |
| 로지스틱 회귀 (2) | 2024.12.20 |
| 다중 회귀 알고리즘 (0) | 2024.12.20 |
| 선형 회귀 알고리즘 (0) | 2024.12.20 |







댓글