헤론의 공식 유도. (세변의 길이로 넓이 구하기)
드디어 여기까지 도달했다.
필자의 블로그의 이전 글을 보면
제1 코사인 법칙,
https://alpaca-code.tistory.com/103(제1코사인 법칙 유도)
제 1 코사인 법칙.
원래 제 2 코사인 법칙 까지 한번에 해보려고 했지만 지금이 새벽 2시 30분 이라 그런지 조금 졸려서 제 1 코사인 법칙 부터 해보겠다. 결국 목표는 헤론의 공식(세변만으로 삼각형 넓이 구하기)
alpaca-code.tistory.com
제2 코사인 법칙을 다룬 것을 볼 수 있다.
https://alpaca-code.tistory.com/104(제2코사인 법칙 유도)
제 2 코사인 법칙.
전 글에서 제 1 코사인 법칙을 유도 해 보았다. 이번엔 제 2 코사인 법칙을 유도 해보겠다. https://alpaca-code.tistory.com/103(이전글-제1코사인법칙) 제 1 코사인 법칙. 원래 제 2 코사인 법칙 까지 한번에
alpaca-code.tistory.com
사실 이 모든 것은
헤론의 공식 유도를 위한 빌드업이었다.
바로 시작해보겠다.
먼저 제2 코사인 법칙을 가져와준다.
a² = b² + c² -2bc cos A
b² = c² + a² - 2ac cos B
c² = a² + b² - 2ab cos C
이런 식 세 개가 있는데,
우리는 이중 세 번째 식(c²)을 중심으로 알아보겠다.
그리고 항상 잊어선 안될 것은
우리의 기준 삼각형이다.
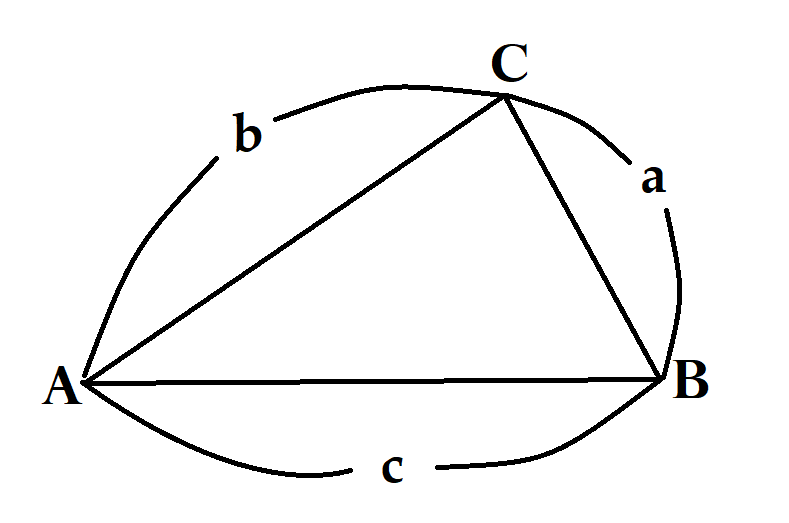
우리는 이런 삼각형에서 모든 것을 유도한 것이다.
잊지 않길 바라며,
시작하겠다. 우선, cos C를 좌변으로 이동시켜
cos C를 구하는 식으로 바꿔준다.
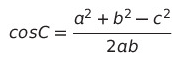
그럼 이렇게 나타내 줄 수 있다.
여기서 우리는 다른 사실을 하나 더 이용해야 한다.
sin² C + cos² C = 1
아주 중요한 Sin과 Cos의 기본 특성이다.
우리는 이 식의 cos² C에
제2 코사인 법칙으로부터 유도한
cos C를 넣고,
sin² C 가 무엇인지 알아야만 한다.
sin² C를 구하기 위해 모두 우변으로 넘기면,
sin² C = 1 - Cos² C이다.
이를 합차 공식에 의해 풀어주면,
sin² C = (1 + cos C) x (1 - cos C)
이렇게 서술할 수 있다.
위 그림으로 보면,
cos C가 (a² + b² - c²) / 2ab 이기에,
1을 2ab위로 올려주면,
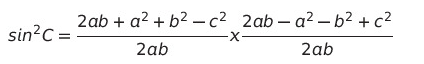
이런 식이 등장하게 된다.
여기서 a² + 2ab + b²은 (a + b) ²으로 묶을 수 있고,
-a² + 2ab -b² 은 -(a - b) ²으로 묶을 수 있기에
다시 한번 정리해주면,
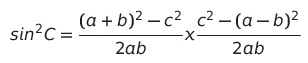
이렇게 묶어 줄 수 있고,
(a + b)를 x로 치환하고 보면
x² - c²으로 또 합차 공식이 성립하기에
두 항 모두 그런 식으로 다시 정리해주면,
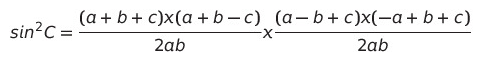
이렇게 정리된다.
이 정도면 많이 깔끔해진 게 보이는가?
이제 두 항을 곱하여 하나로 만들어준다.
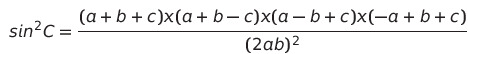
이렇게 정리할 수 있게 되었으면,
루트를 취하여
각 변의 제곱을 제거해 준다.
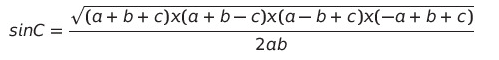
여기까지 이해했다면, 거의 다 왔다고 봐도 무방하다.
삼각형의 공식 중에는 밑변 x 높이 x 0.5(2분의 1)도 있지만,
삼각비를 이용하는
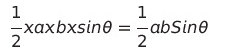
이런 공식도 있다.
위의 두 사진을 자세히 보다 보면,
연관성이 있지 않은가?
그렇다 우리는 사인을 구했고,
넓이 공식에 사인이 들어간다.
이걸 토대로 우리가 구한 사인을
저 넓이 공식에 적용해보면,
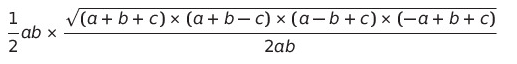
이렇게 나온다.
ab끼리 약분한 뒤, 분모끼리 곱해주면,
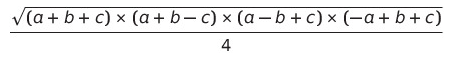
이런 식이 된다.
그렇다 우리는 세 변의 길이,
a, b, c로 삼각형의 넓이를 구하는 공식을
찾은 것이다.
물론 저 식도 맞지만,
인터넷에 헤론의 공식이라고 쳐보면,
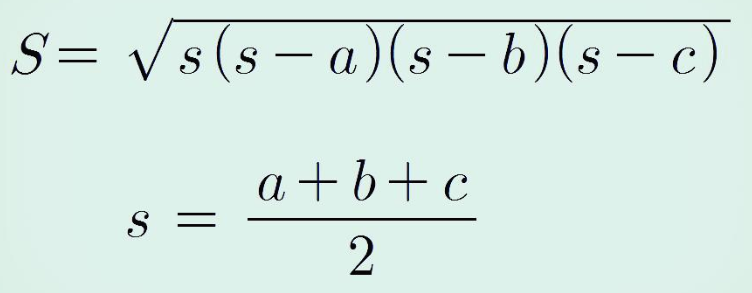
우리가 구한 공식과는 달라 보이는
조금 더 편해 보이는 식을 발견할 수 있다.
이건 사실 S라는 미지수를 새로 만들어서
계산을 편하게 하려고
우리가 구한 식을 살짝 변형한 것일 뿐이다.
그래도 저 식이 대중화되어있으니
저것도 한번 유도해보자.
먼저 a + b + c를 2s라고 쳐보자.
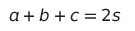
그렇다면, a + b - c는 몇 s 겠는가?
그렇다. a + b + c - 2c와 같기 때문에,
2s - 2c라고 정리해줄 수 있다.
같은 방법으로, 다른 항들도 s로 치환하면
a + b + c = 2s
a + b - c = 2s - 2c
a - b + c = 2s - 2b
-a + b + c = 2s - 2a
이렇게 정리해줄 수 있겠다.
이걸 앞선 공식에 적용해보면,
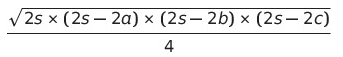
이렇게 바꿔 줄 수 있다.
이제 각 항에서 공통 인수인 2를 빼면,
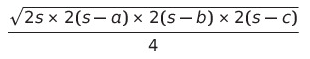
이렇게 바꿔줄 수 있고,
2 끼리 먼저 곱해주면,
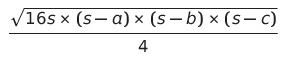
이렇게 되고,
16은 4의 제곱 즉, 제곱수이기에
루트 밖으로 꺼내와 주면,
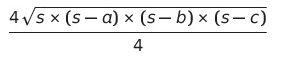
이렇게 되고,
밑의 분수와 분자끼리 약분해주면,
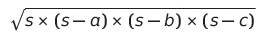
여기까지 나타나게 되고,
앞서 본 공식과 동일하게 하기 위해
곱하기 기호를 생략해주면,
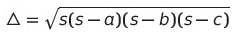
어디서 본 식이 나온다.
하지만 우리는 2s를 a + b + c로 치환했기 때문에,
s는 a + b + c를 2로 나눈 값인,
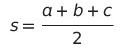
여기까지.
이렇게 헤론의 공식을 유도할 수 있다.
남들처럼 한 장으로 정리해보자면,
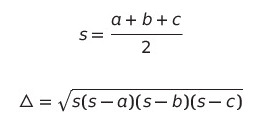
이렇게 정리할 수 있겠다.
세 변의 길이만으로 넓이를 구하는 공식이 있다는
상식 밖의 내용에 감탄하여
며칠 동안 찾아봐가며 이해하였다.
수학자들은 정말 천재인 것 같다는 생각이 다시 한번 든다.
여기까지 헤론의 공식을 유도해봤다.
이상으로 도움이 되었길 바라며,
모르는 점이 있다면 댓글로 써줘도 좋다.
끝.